Overview of this class

• Fixed effects vs random effects
• Mixed effects models
• Diagnostics

What is a multilevel model?

• Observations are not independent, but belong to a hierarchy
• Example: individual level demographics (age, gender), and school level information (location, cours offerings, classroom resources)
• Multilevel model enables fitting different types of dependencies

Fixed vs random

• Fixed effects can be used when you know all the categories, e.g. age, gender, smoking status
• Random effects are used when not all groups are captured, and we have a random selection of the groups, e.g. individuals (if you have multiple measurements), schools, hospitals

Mixed effects models - a type of multilevel model

For data organized in $g$ groups, consider a continuous response linear mixed-effects model (LME model) for each group $i$, $i=1,\dots ,g$:

$$\underset{(n_i\times 1)}{y_i}=\underset{(n_i\times p)}{X_i}\underset{(p\times 1)}{\beta }+\underset{(n_i\times q)}{Z_i}\underset{(q\times 1)}{b_i}+\underset{(n_i\times 1)}{{\epsilon }_i}$$

• $y_i$ is the vector of outcomes for the $n_i$ level-1 units in group $i$
• $X_i$ and $Z_i$ are design matrices for the fixed and random effects
• $\beta$ is a vector of $p$ fixed effects governing the global mean structure
• $b_i$ is a vector of $q$ random effects for between-group covariance
• ${\epsilon }_i$ is a vector of level-1 error terms for within-group covariance

Example

• Data: $radon$, 919 owner-occupied homes in 85 counties of Minnesota. Available in the HLMdiag package
• Response: $log.radon$
• Fixed: $storey$ (categorical)
• Covariate: $uranium$ (quantitative)
• Random: $county$ (house is a member of county)

## Observations: 919
## Variables: 5
## $ log.radon   <dbl> 0.7885, 0.7885, 1.0647, 0.0000, 1.1314, 0.9163, 0....
## $ storey      <int> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
## $ uranium     <dbl> -0.689, -0.689, -0.689, -0.689, -0.847, -0.847, -0...
## $ county      <int> 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,...
## $ county.name <fctr> AITKIN, AITKIN, AITKIN, AITKIN, ANOKA, ANOKA, ANO...

Take a look

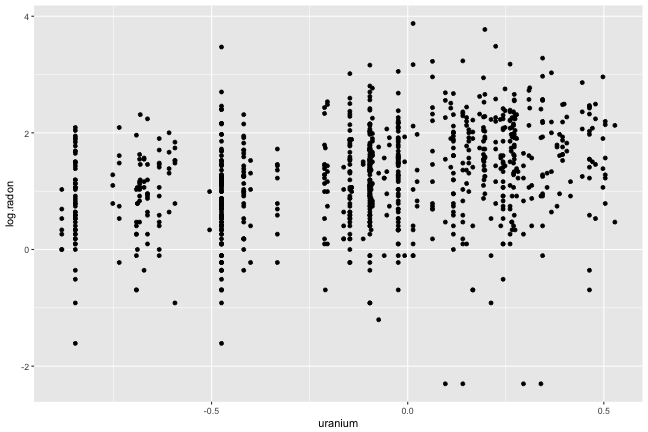
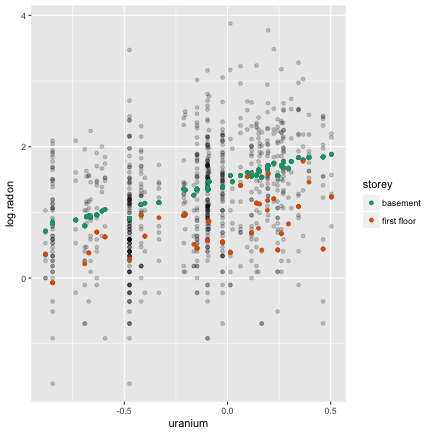
Plot of response vs covariate. What do you see?

Here's what we see

• Vertical stripes: each county is represented by an average uranium value
• Weak linear association, lots of variation for houses within county
• Four points inline horizontally at the base (be suspicious)
• Some counties only have 2, 3 points
• Scales?

Pre-processing

• Counties with less than 4 observations removed
• Four flat-line observations removed, really suspect these were erroneously coded missing values

Look again

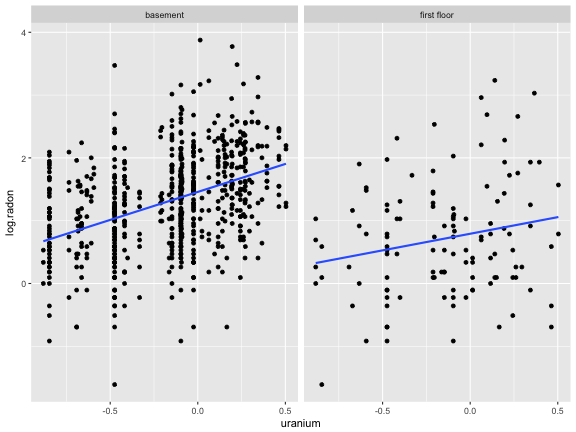
Fit a simple model

$$log.radon={\beta }_0+{\beta }_{1}storey+{\beta }_{2}uranium+\epsilon$$

## 
## Call:
## glm(formula = log.radon ~ storey + uranium, data = radon_sub)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.6610  -0.4928   0.0191   0.4745   2.4205  
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         1.4483     0.0313   46.25  < 2e-16 ***
## storeyfirst floor  -0.6112     0.0733   -8.34  3.3e-16 ***
## uranium             0.8359     0.0742   11.26  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 0.547)
## 
##     Null deviance: 538.51  on 795  degrees of freedom
## Residual deviance: 434.02  on 793  degrees of freedom
## AIC: 1784
## 
## Number of Fisher Scoring iterations: 2

Fit an interaction term

## 
## Call:
## glm(formula = log.radon ~ storey * uranium, data = radon_sub)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.6445  -0.4898   0.0131   0.4653   2.4369  
## 
## Coefficients:
##                           Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 1.4580     0.0318   45.91  < 2e-16 ***
## storeyfirst floor          -0.6659     0.0796   -8.37  2.7e-16 ***
## uranium                     0.8909     0.0805   11.07  < 2e-16 ***
## storeyfirst floor:uranium  -0.3620     0.2066   -1.75     0.08 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 0.546)
## 
##     Null deviance: 538.51  on 795  degrees of freedom
## Residual deviance: 432.34  on 792  degrees of freedom
## AIC: 1783
## 
## Number of Fisher Scoring iterations: 2

What does this model look like?

Mixed effects model

$$log.rado{n}_{ij}={\beta }_0+{\beta }_{1}store{y}_{ij}+{\beta }_{2}uraniu{m}_i+b_{0i}+b_{1i}store{y}_{ij}+{\epsilon }_{ij}$$

$$i=1,...,\#counties;j=1,...,n_i$$

library(lme4)
radon_lmer <- lmer(log.radon ~ storey + uranium + 
  (storey | county.name), data = radon_sub)
summary(radon_lmer)
radon_lmer_fit <- augment(radon_lmer)

Examining the model output: fixed effects

Fixed effects:
                    Estimate Std. Error t value
(Intercept)          1.48066    0.03856   38.40
storeyfirst floor   -0.59011    0.11246   -5.25
uranium              0.84600    0.09532    8.88

How do these compare with the simple linear model estimates?

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        1.44830    0.03131  46.254  < 2e-16 ***
storeyfirst floor -0.61125    0.07332  -8.337 3.35e-16 ***
uranium            0.83591    0.07422  11.262  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Examining the model output: random effects

Random effects:
 Groups      Name                Variance Std.Dev. Corr
 county.name (Intercept)         0.01388  0.1178       
             storeyfirst floor   0.22941  0.4790   0.02
 Residual                        0.50694  0.7120       
Number of obs: 796, groups:  county.name, 46

This is saying that the variance of the estimates for first floor observations is larger than the storey.

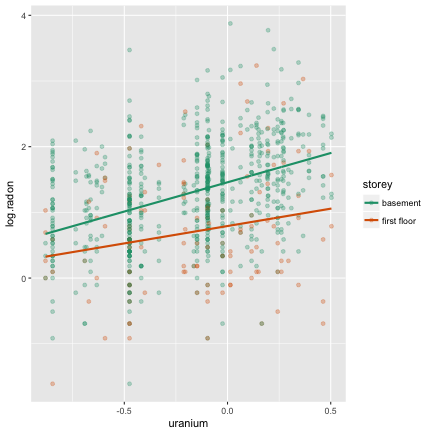
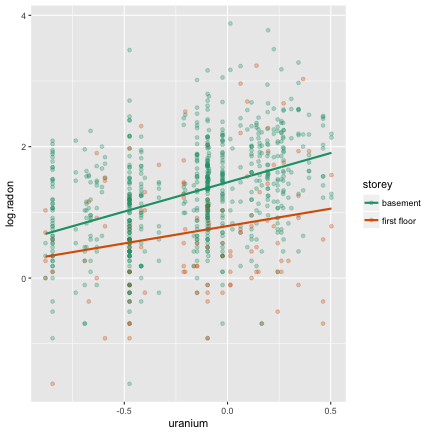
What it looks like

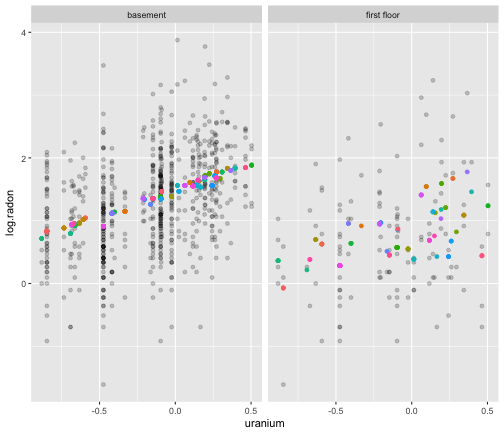
Or like this

Assumptions

Recall:

$$\underset{(n_i\times 1)}{y_i}=\underset{(n_i\times p)}{X_i}\underset{(p\times 1)}{\beta }+\underset{(n_i\times q)}{Z_i}\underset{(q\times 1)}{b_i}+\underset{(n_i\times 1)}{{\epsilon }_i}$$

• $b_i$ is a random sample from $N(0,D)$ and independent from the level-1 error terms,
• ${\epsilon }_i$ follow a $N(0,{\sigma }^2{R}_i)$ distribution
• $D$ is a positive-definite $q\times q$ covariance matrix and $R_i$ is a positive-definite $n_i\times n_i$ covariance matrix

Extract and examine level-1 residuals

${\epsilon }_i\sim N(0,{\sigma }^2{R}_i)$

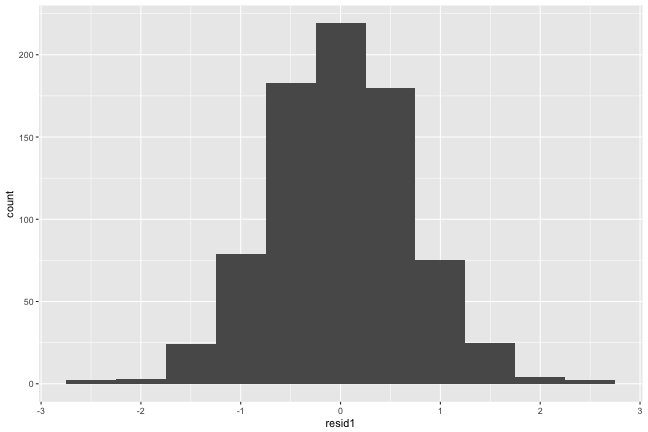
Level-1 (observation level) look normal.

QQ-plot

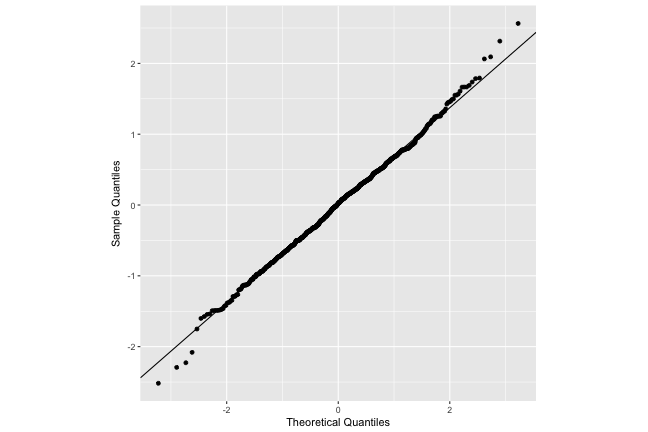
Level-1 (observation level) do look nearly normal.

Examine within group

Summary statistics

## # A tibble: 20 x 4
##    county.name        m     s     n
##         <fctr>    <dbl> <dbl> <int>
##  1       ANOKA  0.05096 0.719    52
##  2    BELTRAMI  0.33508 0.867     7
##  3  BLUE EARTH  0.15188 0.562    14
##  4     CARLTON -0.19433 0.651    10
##  5      CARVER  0.32231 0.924     5
##  6        CASS  0.38263 0.504     5
##  7     CHISAGO  0.15472 0.845     6
##  8        CLAY  0.16252 0.885    14
##  9   CROW WING  0.04541 0.679    12
## 10      DAKOTA -0.04153 0.717    63
## 11     DOUGLAS  0.07803 0.329     9
## 12   FARIBAULT -0.42081 0.311     5
## 13    FREEBORN  0.31357 0.723     9
## 14     GOODHUE  0.15537 0.719    14
## 15    HENNEPIN -0.00737 0.662   105
## 16     HOUSTON -0.13553 0.483     6
## 17     HUBBARD -0.02903 0.712     5
## 18      ITASCA  0.00484 0.584    11
## 19     JACKSON  0.24493 0.689     5
## 20 KOOCHICHING -0.10696 0.466     7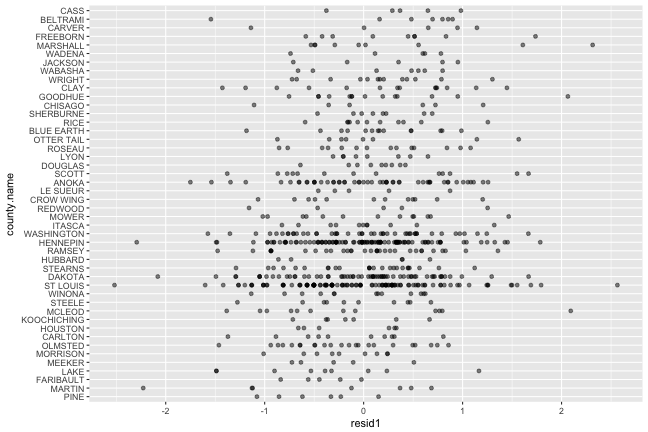

Learn

There is some difference on average between counties, which means that residuals still have some structure related to the county location.

Normality tests

Anderson-Darling, Cramer-von Mises, Lilliefors (Kolmogorov-Smirnov)

## 
##     Anderson-Darling normality test
## 
## data:  radon_lmer_fit$resid1
## A = 0.4, p-value = 0.4

all believe that the residuals are consistent with normality.

Conclusion about level-1 residuals

The assumption:

$${\epsilon }_i\sim N(0,{\sigma }^2{R}_i)$$

is probably ok, at the worst it is not badly violated.

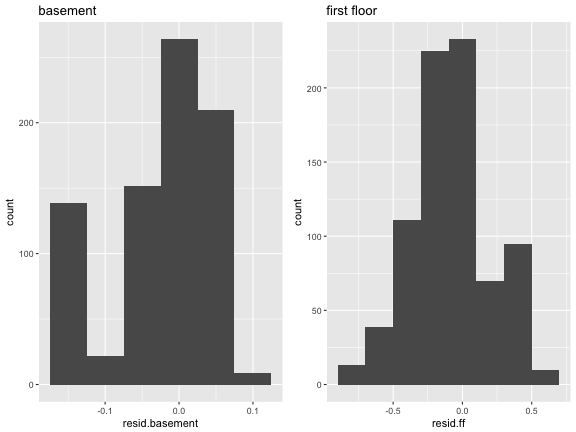
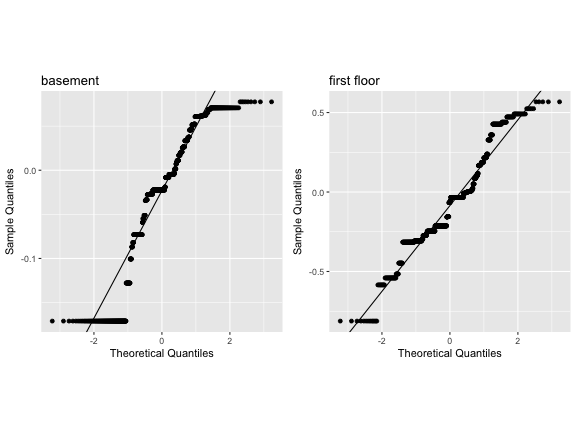
Random effects

$$b_i\sim N(0,D),i=1,\dots g$$

where $D$ allows for correlation between random effects within group, and these should be independent from the level-1 error

We have both intercepts (basement) and slopes (first floor)

Should be no correlation

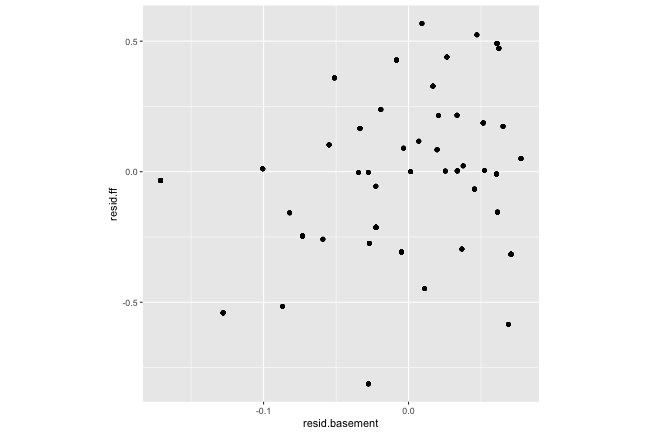
Fitted vs Observed

Plotting the observed vs fitted values, gives a sense for how much of the response is explained by the model. Here we can see that there is still a lot of unexplained variation.

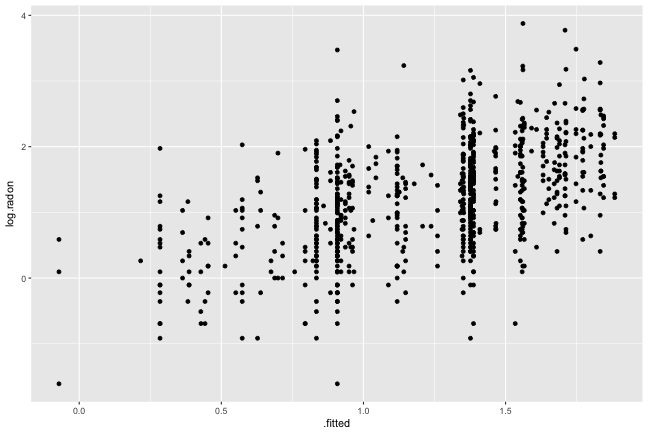
Goodness of fit

From the linear model

##   null.deviance df.null logLik  AIC  BIC deviance df.residual
## 1           539     795   -887 1783 1806      432         792

From the random effects model

##   sigma logLik  AIC  BIC deviance df.residual
## 1 0.712   -885 1784 1817     1760         789

Hmmm... deviance looks strange! Compute sum of squares of residuals instead:

## [1] 387

Which model is best?

Influence

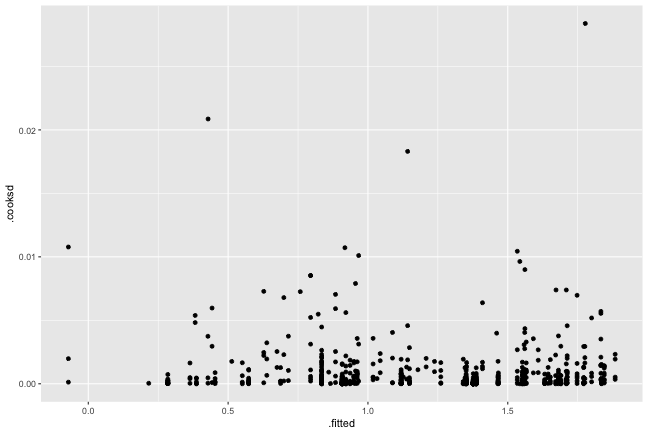
No overly influential observations

Resources

• HLMDiag package explanation
• HLM package